Приклади роботи в MathCAD
Більшість обчислень у Mathcad можна виконати трьома способами:
– Вибором операції в меню, за допомогою
– кнопкових панелей інструментів, звернення до відповідних функцій.
Майже всі операції закріплені за пунктами меню дублюються відповідними кнопками панелей інструментів. Щоб повернутись до вбудованої функції, можна вставити функцію в робочий документ, вибравши потрібне ім’я зі списку функцій, можна ввести ім’я функції з клавіатури або, для функцій, що найчастіше використовуються, вставити ім’я функції клацанням по кнопці в панелі інструментів. Таким чином, у всіх трьох випадках дотримується той самий порядок дій:
а) вибір операції здійснюється клацанням миші по пункту меню або по кнопці в панелі інструментів, після чого, якщо потрібно, користувач отримує доступ до спадного меню або додаткової панелі;
б) коли вибрано операцію, користувач вводить необхідну інформацію у вікні діалогу або заповнює позначені поля в полі введення, яке відкривається безпосередньо в робочому документі.
Розглянемо зміст кожного пункту меню і опишемо правила виконання операцій, що найчастіше використовуються.
Ранжовані змінні в MathCAD
У пакеті MathCAD існує можливість виконувати обчислення, що повторюються. Для цього використовується спеціальний тип змінних – ранжовані змінні чи дискретні аргументи.
Ранжована змінна приймає діапазон значень, наприклад, усі цілі числа від 0 до 10. Якщо у виразі є дискретний аргумент (ранжована змінна), то MathCad обчислює вираз стільки разів, скільки значень містить цей дискретний аргумент.
Функції в MathCAD
Найчастіше у MathCAD виникає потреба у використанні елементарних функцій. Щоб використовувати функцію у виразі, треба визначити значення вхідних параметрів у дужках після імені функції. Аргумент і значення елементарних функцій може бути дійсними чи комплексними числами. Усі кути вимірюються у радіанах.
Функції, задані із застосуванням звичайного знака присвоювання, є локальними, тому вони мають бути задані в документі до використання.
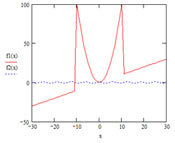
Графіки в декартовій системі координат MathCAD
MathCAD дозволяє будувати двовимірні графіки в декартовій та полярній системах координат, а також тривимірні графіки, включаючи зображення поверхонь, карти ліній рівня та ряд інших. Доступ до цієї операції здійснюється через панель Graph або через пункт меню Graphics. В останніх версіях пакета доступ до опції Graph реалізується через пункт меню Insert.
Графіки поверхонь в MathCAD
На відміну від двовимірних графіків, які використовують дискретні аргументи та функції, графік поверхні потребує матриці значень. Елементи матриці представляються на графіку як висоти, розташовані вище або нижче за площину Oxy. Типовий поверхневий графік показує значення функції двох змінних.
Розв’язання нелінійних рівнянь у MathCAD
Багато рівнянь, наприклад, трансцендентні, не мають аналітичних рішень. Однак вони можуть бути вирішені чисельно ітераційними методами із заданою похибкою (метод поділу відрізка навпіл, метод хорд, метод дотичних і т.д.). Для вирішення одного рівняння f(x)=0 з одним невідомим у Mathcad використовується функція root:
root (вираз, ім’я_змінної)
Першим аргументом є або функція, визначена десь у робочому документі, або вираз для обчислення скалярного значення. Другий аргумент – ім’я змінної, що використовується у виразі.
Цій змінній перед викликом функції root необхідно надати числове значення. Mathcad використовує його як початкове наближення під час пошуку кореня. Функція root повертає значення змінної, при якому вираз звертається до 0. Mathcad дозволяє знаходити як речові, так і комплексні корені. Для визначення речових коренів початкове наближення має бути речовим, для визначення комплексного коріння – комплексним.
Точність розрахунків встановлюється системною змінною TOL, значення якого можна змінити, вибравши команди Математика-Опції-Вбудовані змінні.
Якщо Matcad не може знайти коріння, з’являється повідомлення про помилку. Ця помилка може бути викликана причинами:
– Рівняння не має коренів;
– коріння рівняння розташоване далеко від початкового наближення;
– вираз має локальні екстремуми між початковим наближенням та корінням;
– вираз має розриви між початковим наближенням та корінням;
– Вираз має комплексний корінь, але початкове наближення було речовим (або навпаки).
Щоб уникнути помилок, рекомендується дослідити графік функції f(x). Він дозволяє з’ясувати наявність коренів рівняння f(x)=0 і, якщо вони є, визначити приблизно їх значення.
Якщо потрібно знайти кілька коренів рівняння, потрібно кілька разів запустити функцію root. При цьому можна використовувати два підходи:
1. Побудувати графік функції f(x), визначити відрізки локалізації коренів і кілька разів запустити функцію root з різними початковими наближеннями (як початкове наближення можна вибрати один з кінців відрізка локалізації коренів).
2. Знайти один із коренів рівняння, задавши довільне початкове наближення. Для рівняння f(x) з відомим коренем a знаходження додаткових коренів еквівалентно пошуку коренів рівняння h(x)=0 де h(x)=f(x)/(x-a). Подібний прийом зручний для знаходження коріння рівняння, розташованого близько один до одного).
Розв’язання трансцендентних рівнянь у MathCAD
1. Відокремити коріння рівняння графічним способом на заданому інтервалі: привести рівняння до виду f (x) = 0 і задати функцію лівої частини рівняння, побудувати графік функції на зазначеному інтервалі, за графіком визначити початкове наближення кореня (коренів), заносячи в змінні x1 (x2).
2. Для кожного початкового наближення кореня знайти з використанням функції root рішення рівняння.
Вирішення систем нелінійних рівнянь у MathCAD
Система Mathcad дозволяє вирішувати системи рівнянь. Максимальна кількість рівнянь і змінних дорівнює 200. Для цього використовується спеціальний обчислювальний блок, в якому після службового слова Given задаються рівняння системи та різні обмеження у вигляді нерівностей. Блок закінчується зверненням до функції пошуку рішення Find:
Given
Рівняння та нерівності
Вираз із Find(x,y)
Параметрами функції Find є змінні, які підбираються в процесі розв’язання так, щоб задовольнялися рівняння та нерівності системи. Попередньо всім змінним перед Given необхідно присвоїти початкові значення. При заданні рівнянь використовують спеціальний жирний знак рівності, який набирається комбінацією клавіш Ctrl=. Обмежувальні умови задаються за допомогою операторів відносин, які вибираються на панелі Булеве.