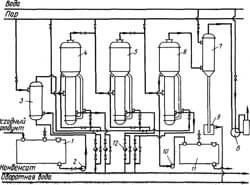
 Примеры работы в MathCAD
Примеры работы в MathCAD
Большинство вычислений в Mathcad можно выполнить тремя способами:
— выбором операции в меню, с помощью
— кнопочных панелей инструментов, обращением к соответствующим функциям.
Почти все операции, закрепленные за пунктами меню, дублируются соответствующими кнопками панелей инструментов. Для обращения к встроенной функции можно вставить функцию в рабочий документ, выбрав нужное имя из списка функций, можно ввести имя функции с клавиатуры или, для наиболее часто используемых функций, вставить имя функции щелчком по кнопке в панели инструментов. Таким образом, во всех трех случаях соблюдается один и тот же порядок действий:
а) выбор операции производится щелчком мыши по пункту меню или по кнопке в панели инструментов, после чего, если нужно, пользователь получает доступ к ниспадающему меню или к дополнительной панели;
б) когда операция выбрана, пользователь вводит необходимую информацию в окне диалога или заполняет помеченные поля в поле ввода, которое открывается непосредственно в рабочем документе.
Рассмотрим содержание каждого пункта меню и опишем правила выполнения наиболее часто используемых операций.
Ранжированные переменные в MathCAD
В пакете MathCAD существует возможность выполнять повторяющиеся вычисления. Для этого используется специальный тип переменных – ранжированные переменные, или дискретные аргументы.
Ранжированная переменная принимает диапазон значений, например, все целые числа от 0 до 10. Если в выражении присутствует дискретный аргумент (ран-жированная переменная), то MathCad вычисляет выражение столько раз, сколько значений содержит этот дискретный аргумент.
Функции в MathCAD
Наиболее часто в MathCAD возникает необходимость в использовании элементарных функций. Чтобы использовать функцию в выражении, надо определить значения входных параметров в скобках после имени функции. Аргумент и значение элементарных функций могут быть действительными или комплексными числами. Все углы измеряются в радианах.
Функции, заданные с применением обычного знака присваивания, являются локальными, поэтому они должны быть заданы в документе до того, как будут использованы.
Графики в декартовой системе координат MathCAD
MathCAD позволяет строить двумерные графики в декартовой и полярной системах координат, а также трехмерные графики, включая изображения поверхностей, карты линий уровня и ряд других. Доступ к данной операции осуществляется через панель Graph, либо через соответствующий пункт меню Graphics. В последних версиях пакета доступ к опции Graph реализуется через пункт меню Insert.
Графики поверхностей в в MathCAD
В отличие от двумерных графиков, которые используют дискретные аргументы и функции, график поверхности требует матрицы значений. Элементы матрицы представляются на графике как высоты, расположенные выше или ниже плоскости Oxy. Типичный поверхностный график показывает значения функции двух переменных.
Решение нелинейных уравнений в MathCAD
Многие уравнения, например, трансцендентные, не имеют аналитиче-ских решений. Однако они могут быть решены численно итерационными методами с заданной погрешностью (метод деления отрезка пополам, метод хорд, метод касательных и т.д.). Для решения одного уравнения f(x)=0 с одним неизвестным в Mathcad используется функция root:
root(выражение, имя_переменной)
Первый аргумент есть или функция, определенная где-либо в рабочем документе, или выражение для вычисления скалярного значения. Второй аргумент – имя переменной, которое используется в выражении.
Этой переменной перед вызовом функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня. Функция root возвращает значение переменной, при котором выражение обращается в 0. Mathcad позволяет находить как вещественные, так и комплексные корни. Для определения вещественных корней начальное приближение должно быть вещественным, для определения комплексных корней – комплексным.
Точность расчетов устанавливается системной переменной TOL, значе-ние которого можно изменить, выбрав команды Математика-Опции-Встроенные переменные.
Если Matcad не может найти корень, появляется сообщение об ошибке. Эта ошибка может быть вызвана причинами:
— уравнение не имеет корней;
— корни уравнения расположены далеко от начального приближения;
— выражение имеет локальные экстремумы между начальным приближением и корнями;
— выражение имеет разрывы между начальным приближением и корнями;
— выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).
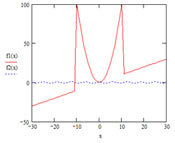
Чтобы избежать ошибок, рекомендуется предварительно исследовать график функции f(x). Он позволяет выяснить наличие корней уравнения f(x)=0 и, если они есть, определить приближенно их значения.
Если необходимо найти несколько корней уравнения, требуется несколько раз запустить функцию root. При этом можно использовать два подхода:
1. Построить график функции f(x), определить отрезки локализации корней и несколько раз запустить функцию root с разными начальными приближениями (в качестве начального приближения можно выбрать один из концов отрезка локализации корней).
2. Найти один из корней уравнения, задав произвольное начальное приближение. Для уравнения f(x) с известным корнем a нахождение дополнительных корней эквивалентно поиску корней уравнения h(x)=0, где h(x)=f(x)/(x-a). Подобный прием удобен для нахождения корней уравнения, расположенных близко друг к другу).
Решение трансцендентных уравнений в MathCAD
1. Отделить корни уравнения графическим способом на заданном интервале: привести уравнение к виду f (x)=0 и задать функцию левой части уравне¬ния, построить график функции на указанном интервале, по графику определить начальное приближение корня (корней), занося в переменные x1 (x2, …).
2. Для каждого начального приближения корня найти с использованием функ¬ции root решение уравнения.
Решение систем нелинейных уравнений в MathCAD
Система Mathcad дает возможность решать системы уравнений. Макси-мальное количество уравнений и переменных равно 200. Для этого используется специальный вычислительный блок, в котором после служебного слова Given задаются уравнения системы и различные ограничения в виде неравенств. Блок заканчивается обращением к функции поиска решения Find:
Given
Уравнения и неравенства
Выражение с Find(x,y)
Параметрами функции Find являются переменные, которые подбираются в процессе решения так, чтобы удовлетворялись уравнения и неравенства системы. Предварительно всем переменным перед Given необходимо присвоить начальные значения. При задании уравнений используется специальный жирный знак равенства, который набирается комбинацией клавиш Ctrl=. Ограничительные условия задаются с помощью операторов отношений, выбираемых на панели Булевое.